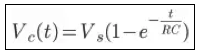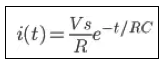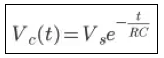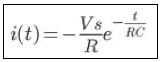Pembelajaran | Blog Akademik Muchlas

Produk Buku 2020: Monograf Pengembangan Perangkat Pembelajaran Sistem Kendali Motor Listrik Berkinerja Tinggi

17. August 2020 · Write a comment · Categories: Aktivitas Akademik, Pembelajaran

Laboratorium merupakan fasilitas penting dan sangat dibutuhkan dalam mendukung kegiatan pembelajaran praktik di lingkungan pendidikan tinggi teknik baik program akademik maupun vokasi. Keterbatasan peralatan yang tersedia di laboratorium dan adanya kebutuhan akan perangkat praktik yang fleksibel, efisien dan aman, khususnya dalam bidang pengendalian motor listrik berkinerja tinggi telah mendorong penulisan monograf ini. Kajian ini secara detil mendeskripsikan proses pengembangan perangkat pembelajaran dalam bentuk simulator sistem kendali motor berkinerja tinggi yang di dalamnya terdapat unit soft-starter dan unit stall detection berbasis perangkat lunak SIMULINK dari Matlab. Selain itu, monograf ini juga menyediakan referensi berupa informasi hasil uji kinerja dan persepsi pengguna dosen, guru dan mahasiswa terhadap penggunaan perangkat pembelajaran yang dikembangkan oleh penulis sebagai peneliti.

Monograf ini dapat dimanfaatkan oleh dosen di lingkungan program studi Teknik Elektro dan guru Sekolah Menengah Kejuruan (SMK) sebagai referensi untuk merancang kegiatan pembelajaran di kelas dengan pendekatan demonstrasi, maupun praktik di laboratorium (pengganti praktik hands-on) secara simulatif untuk materi pengendalian motor induksi tiga fase menggunakan thyristor.

Topik-topik praktik yang dapat diselenggarakan dengan simulator yang ada di dalam monograf ini antara lain karakteristik dinamis motor induksi tiga fase dengan catu direct-on-line supplied, soft starter dan stall detector, serta analisis bentuk gelombang tegangan dan arus motor dengan pengendali tegangan oleh thyristor. Selain itu, monograf juga dapat digunakan sebagai referensi bagi peneliti yang tertarik melakukan riset pengembangan perangkat pembelajaran yang terkait dengan implementasi simulator berbasis SIMULINK dari Matlab, khususnya untuk bidang pengendalian motor induksi berkinerja tinggi dengan menggunakan piranti thyristor sebagai voltage controller.

Klik pada gambar untuk download buku.

Sitasi dalam format APA:

Muchlas. (2020). Monograf pengembangan perangkat pembelajaran sistem kendali motor listrik berkinerja tinggi. Yogyakarta: UAD Press.

Produk Artikel Ilmiah 2020: Perangkat Pembelajaran Laboratorium Virtual Elektronika Dasar Berbasis Perangkat Lunak Pspice

15. May 2020 · Write a comment · Categories: Aktivitas Akademik, Pembelajaran

Saat ini ketersediaan modul-modul untuk mendukung praktik elektronika dasar berbasis laboratorium virtual masih belum dapat memenuhi kebutuhan. Studi pada artikel yang diterbitkan melalui JOVES ini ditujukan untuk menghasilkan perangkat pembelajaran yang layak digunakan sebagai pendukung praktik elektronika dasar berbasis program aplikasi PSPICE. Untuk memperoleh informasi kinerja rangkaian atau kelayakan produk, dilakukan analisis perbandingan antara karakteristik yang diperoleh melalui eksperimen menggunakan PSPICE terhadap watak teoritiknya. Hasil penelitian menunjukkan bahwa semua modul yang dikembangkan dapat menampilkan karakteristik yang sama dengan watak teoritiknya, hal ini menunjukkan bahwa modul-modul tersebut memiliki kinerja yang sangat baik sehingga layak digunakan sebagai media praktik elektronika dasar menggunakan laboratorium virtual berbasis PSPICE. Produk yang dihasilkan berupa rangkaian elektronik dalam format schematic dari PSPICE sebanyak 31 buah, untuk mendukung praktik elektronika dasar yang meliputi topik: Pengisian dan Pengosongan Kapasitor, Rangkaian RC, Karakteristik Diode, Rangkaian Pembentuk Gelombang, Rangkaian Penyearah, Rangkaian Penjepit dan Pengganda Tegangan, Karakteristik Transistor, dan Rangkaian Amplifier Transistor.

Klik pada gambar untuk download artikel.

Sitasi dalam format APA:

Muchlas & Budiastuti, P. 2020. Development of learning devices of basic electronic virtual laboratory based on PSPICE software. Journal of Vocational Education Studies (JOVES), 3(1), 1-18.

Produk Terbaru Saya 2019: Lab Virtual Elektronika Dasar Berbasis PSPICE

05. April 2019 · Write a comment · Categories: Aktivitas Akademik, Pembelajaran

Pada Maret 2019, saya telah selesai menciptakan lab virtual untuk praktik Elektronika Dasar menggunakan aplikasi PSPICE. Proyek ini dilatarbelakangi oleh kenyataan bahwa saat ini ketersediaan modul-modul untuk mendukung praktik elektronika dasar berbasis laboratorium virtual masih belum dapat memenuhi kebutuhan. Mengapa harus menggunakan lab virtual? Perkembangan teknologi informasi yang sangat pesat telah mendisrupsi landscape laboratorium teknik termasuk elektronika dasar, yang semula hanya mengandalkan peralatan-peralatan real, saat ini muncul kebutuhan untuk mengintegrasikan kegiatan-kegiatan hands-on activity dengan online activity dalam sebuah blanded learning penyelenggaraan praktik. Produk yang saya ciptakan ini memperkaya implementasi lab virtual untuk mendukung online activity menggunakan aplikasi yang handal dan mudah dioperasikan dalam praktik elektronika dasar.

Produk ini dapat digunakan oleh dosen/mahasiswa jurusan Teknik Elektro dan jurusan sejenis serta guru/siswa SMK untuk mengajar/belajar Elektronika Dasar. Secara fungsional, produk ini dapat digunakan sebagai media pembelajaran di kelas atau untuk mendukung praktik di laboratorium. Secara lebih detil, spesifikasi produk disajikan pada tabel berikut ini.

Tabel 1. Spesifikasi produk

Screen Shot 2019-07-05 at 7.11.20 AM

Produk ini menyediakan 8 topik praktik elektronika dasar dengan dukungan rangkaian virtual seperti ditunjukkan pada tabel 2.

Tabel 2. Topik dan Rangkaian Virtual Pendukung yang disediakan Produk

Screen Shot 2019-07-05 at 1.25.46 PM

Rangkaian elektronika virtual berbasis PSPICE pada produk ini ditunjukkan melalui gambar berikut ini.

Gambar 1. Rangkaian Pengisian dan Pengosongan Kapasitor, Rangkaian RC, dan Rangkaian Karakteristik Diode

Screen Shot 2019-07-07 at 11.43.50 AM

Gambar 2. Rangkaian Pembentuk Gelombang

Screen Shot 2019-07-07 at 11.48.44 AM

Gambar 3. Rangkaian Penyearah

Screen Shot 2019-07-07 at 11.52.24 AM

Gambar 4. Rangkaian Penjepit dan Pengganda Tegangan Screen Shot 2019-07-07 at 11.56.29 AM

Gambar 5. Karakteristik Transistor dan Rangkaian Penguat

Sedangkan ouput yang dihasilkan oleh rangkaian-rangkaian tersebut disajikan gambar-gambar berikut ini.

1. Pengisian dan Pengosongan Kapasitor

Screen Shot 2019-07-05 at 8.09.21 AM Gambar 6. Kurva tegangan (atas) dan arus (bawah) pengisian kapasitor hasil eksperimen laboratorium virtual SPICE (kiri) dan teoritik (kanan)

Screen Shot 2019-07-05 at 8.11.13 AM Gambar 7. Kurva tegangan (atas) dan arus (bawah) pengosongan kapasitor hasil eksperimen laboratorium virtual SPICE (kiri) dan teoritik (kanan)

2. Rangkaian RC

Screen Shot 2019-07-05 at 8.20.17 AM

Gambar 8. Watak integrator dengan input gelombang kotak (garis tebal: tegangan output; garis tipis: tegangan input)

Screen Shot 2019-07-05 at 8.20.28 AM

Gambar 9. Watak integrator dengan masukan gelombang sinus (garis tebal: tegangan output; garis tipis: tegangan input)

Screen Shot 2019-07-05 at 1.02.19 PM

Gambar 10. Watak diferensiator dengan input gelombang kotak

Screen Shot 2019-07-05 at 1.02.33 PM

Gambar 11. Watak diferensiator dengan input gelombang sinus

Screen Shot 2019-07-05 at 1.17.28 PM

Gambar 12. Respons frekuensi filter low pass dan filter high pass hasil eksperimen dengan PSPICE

3. Karakteristik Diode

Screen Shot 2019-07-07 at 12.28.27 PM

Gambar 13. Hasil pengukuran karakteristik diode 1N4002 menggunakan PSPICE

4. Rangkaian Pembentuk Gelombang

Screen Shot 2019-07-05 at 1.17.51 PM

Gambar 14. Watak rangkaian pembentuk gelombang hasil eksperimen PSPICE

5. Rangkaian Penyearah

Screen Shot 2019-07-05 at 1.18.35 PM Gambar 15. Bentuk gelombang tegangan pada penyearah setengah gelombang hasil eksperimen menggunakan PSPICE dengan beban ringan

Screen Shot 2019-07-05 at 1.19.31 PM

Gambar 16. Bentuk gelombang tegangan pada penyearah gelombang penuh hasil eksperimen dengan PSPICE: (a) beban ringan, dan (b) beban penuh

Screen Shot 2019-07-05 at 1.20.05 PM

Gambar 17. Bentuk gelombang penyearah jembatan dengan beban ringan hasil eksperimen menggunakan PSPICE

Screen Shot 2019-07-07 at 12.48.29 PM

Gambar 18. Bentuk gelombang tegangan rangkaian penyearah filter C Hasil eksperimen menggunakan PSPICE

6. Rangkaian Penjepit dan Pengganda Tegangan

Screen Shot 2019-07-07 at 12.49.56 PM

Gambar 19. Watak rangkaian penjepit hasil eksperimen menggunakan PSPICE dan hasil komputasi teoritik

Screen Shot 2019-07-07 at 12.52.10 PM

Gambar 20. Watak pengganda tegangan dua kali

Screen Shot 2019-07-07 at 12.52.22 PM

Gambar 21. Watak pengganda tegangan empat kali

7. Karakteristik Transistor

Screen Shot 2019-07-07 at 12.58.34 PM

Gambar 22. Karaktersitik transistor 2N2222 hasil eksperimen dengan PSPICE

8. Rangkaian Penguat

Screen Shot 2019-07-07 at 12.59.59 PM

Gambar 23. Respons amplitudo amplifier common emitter untuk V_i=1mV: (a) tanpa kapasitor bypass; (b) dilengkapi kapasitor bypass

Selamat menggunakan!!

Tutorial PSPICE Bagian 2: Rangkaian RC (Time Constant)

27. September 2018 · 4 comments · Categories: Aktivitas Akademik, Pembelajaran

Rangkaian RC merupakan rangkaian elektronika yang tersusun atas komponen resistor (R) dan kapasitor (C) serta dicatu dengan sumber tegangan atau sumber arus. Pada domain waktu, rangkaian RC dapat dimanfaatkan sebagai pendeferensiasi sinyal (rangkaiannya disebut dengan diferensiator) dan rangkaian untuk mengintegralkan sinyal (rangkaiannya disebut dengan integrator). Selain itu, pada domain frekuensi, rangkaian RC dapat diaplikasikan sebagai rangkaian untuk menyeleksi frekuensi dari suatu sinyal. Dengan menggunakan rangkaian RC dapat dibuat filter low pass yang digunakan untuk meloloskan sinyal frekuensi rendah, filter high pass untuk meloloskan sinyal frekuensi tinggi, filter band pass untuk meneruskan sinyal dengan band frekuensi tertentu, dan filter band reject untuk menahan sinyal dengan band frekuensi tertentu.

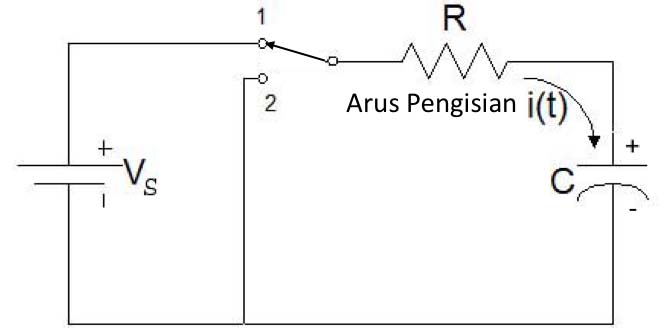
Rangkaian RC Pengisian Kapasitor

Rangkaian RC sederhana terdiri atas satu resistor, satu kapasitor, satu sumber tegangan DC, satu buah saklar dapat ditunjukkan seperti gambar di bawah ini.

Gambar 1. Rangkaian RC Pengisian Kapasitor

Jika saklar diarahkan ke posisi 1 maka akan mengalir arus i(t) mengisi kapasitor C dan dalam keadaan ini dapat ditulis persamaan:

$V_{S}=V_{{R}}+V_{{C}}$

$V_{{s}}=iR+\frac{Q}{C}$

$V_{{s}}=\frac{dQ}{dt}}}R+\frac{Q}{C}$

$\frac{dQ}{dt}}}R=V_{{s}}-\frac{Q}{C}$

$\frac{dQ}{dt}= \frac{1}{R}(V_{{s}}-\frac{Q}{C})$ (persamaan 1)

Persamaan 1 dapat diselesaikan dengan metode pemisahan variabel. Langkah pertama adalah memisahkan notasi-notasi yang berhubungan dengan variabel muatan listrik (Q dan dQ) terhadap notasi yang berhubungan dengan variabel waktu (dt). Pada kasus ini, notasi Q dan dQ ditempatkan pada ruas kiri, sedangkan dt di ruas kanan persamaan, sehingga persamaan 1 dapat diubah bentuknya menjadi persamaan 2 berikut ini.

$\frac{dQ}{(V_{{s}}-\frac{Q}{C})}= \frac{1}{R}dt $ (persamaan 2)

Jika ruas kiri dan ruas kanan dibagi dengan -C, maka persamaan 2 dapat diubah bentuknya menjadi:

$\frac{dQ}{Q-CV_{{s}}}=- \frac{1}{RC}dt $ (persamaan 3)

Pengintegralan ruas kiri dan ruas kanan pada persamaan 3 menghasilkan persamaan:

$\int_{0}^{Q(t)} \frac{dQ}{Q-CV_{{s}}}=- \frac{1}{RC}\int_{0}^{t}dt $ (persamaan 4)

Berdasarkan rumus integral, telah diketahui bahwa $\int_{}^{} \frac{1}{ax+b}dx=\frac{1}{a}ln\left \| ax+b \right \|$ , sehingga persamaan 4 dapat diubah menjadi:

$ln\left \| Q-CV_{s} \right \||_{0}^{Q(t)}=-\frac{t}{RC}\$

$ln\left \{Q(t)-CV_{s} \right \}-ln\left \{ Q(0)-CV_{s} \right \}=- \frac{t}{RC}$

$ln\left \{ Q(t)-CV_{s} \right \}-ln(-CV_{s})=- \frac{t}{RC}$

$ ln(\frac{Q(t)-CV_{s} }{{-CV_{s} }})=- \frac{t}{RC} $

Telah diketahui bahwa $e ^{ln(x)}=x$ , sehingga apabila ruas kiri dan ruas kanan dari persamaan di atas menjadi pangkat dari e, maka akan dihasilkan persamaan:

$e^{ln(\frac{Q(t)-CV_{s} }{{-CV_{s} }})}=e ^{-\frac{t}{RC}}$

$\frac{Q(t)-CV_{s} }{{-CV_{s} }}}=e ^{-\frac{t}{RC}}$

$Q(t)=-CV_{s} e ^{-\frac{t}{RC}}+CV_{s}$

$Q(t)=CV_{s}(1- e ^{-\frac{t}{RC}})$ (persamaan 5)

Oleh karena muatan listrik yang mengisi kapasitor besarnya $Q(t)=CV_{{c}}(t)$ , maka tegangan kapasitor dapat diperoleh dengan melakukan substitusi persamaan ini ke dalam persamaan 5 sehingga diperoleh persamaan:

$CV_{c}(t)=CV_{s}(1- e ^{-\frac{t}{RC}})$

(persamaan 6)

Persamaan 6 menunjukkan besarnya tegangan kapasitor yang merupakan fungsi waktu t, sedangkan persamaan arus yang mengisi kapasitor dapat diturunkan dari persamaan 5. Oleh karena besarnya arus pada proses pengisian kapasitor didefinisikan sebagai besar muatan per satuan waktu, maka persamaan arus dapat diperoleh dengan menurunkan fungsi Q(t) pada persamaan 5 terhadap waktu t. Dengan demikian persamaan arus pada pengisian kapasitor dapat ditulis sebagai berikut.

$i(t)=\frac{dQ(t)}{dt}=\frac{d}{dt}CV_{s}(1- e ^{-\frac{t}{RC}})$

$i(t)=\frac{d}{dt}CV_{s}-CV_{s}\frac{d}{dt} e ^{-\frac{t}{RC}}$

Berdasarkan rumus diferensial, telah diketahui bahwa $\frac{d}{dx} e^{u}= e^{u}\frac{du}{dx}$ , sehingga persamaan dapat diubah menjadi:

$i(t)=0-(CV_{s})(e ^{-\frac{t}{RC}}) (-\frac{1}{{RC}})$

(persamaan 7)

Pada persamaan 6 dan persamaan 7, keterangan untuk setiap notasinya adalah sebagai berikut.

Vc(t) = tegangan pada kapasitor (V)

i(t) = arus yang mengalir pada kapasitor setiap saat (A)

Vs = tegangan sumber (V)

e = bilangan natural=2,72

RC = Konstanta Waktu (time constant) dalam satuan detik (s)

Konstanta waktu diberi simbol $\tau$ (tau), sehingga

(persamaan 8),

dengan R dalam ohm dan C dalam farad. Contoh jika $R=10K\Omega= 10^{4}K\Omega$ dan $C=0,1\mu F= 10^{-7}F$ , maka $\tau=RC= 10^{-3}detik=1ms$ .

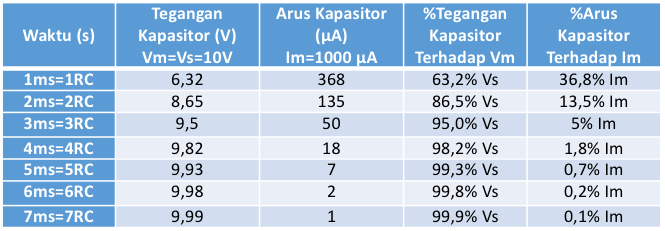
Persamaan 6 dan persamaan 7 menunjukkan besarnya tegangan dan dan arus kapasitor selama komponen tersebut mengalami pengisian muatan. Jika ke dalam kedua persamaan tersebut dimasukkan nilai-nilai variabel t untuk $R=10K\Omega$ dan $C=0,1\mu F$ akan menghasilkan nilai-nilai tegangan dan arus kapasitor seperti ditunjukkan pada tabel 1 berikut ini.

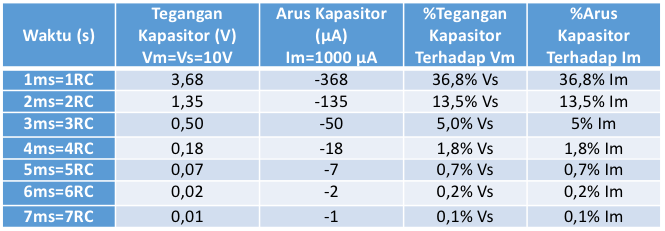
Tabel 1. Nilai tegangan dan arus pada pengisian kapasitor untuk RC=1ms

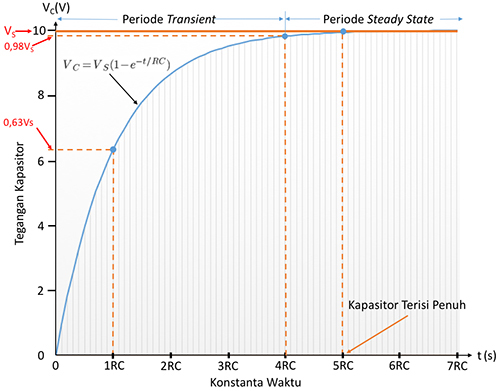
Selanjutnya, jika dilakukan plotting antara Vc versus t akan diperoleh kurva pengisian kapasitor seperti pada gambar 2.

Gambar 2. Kurva tegangan kapasitor versus waktu selama pengisian muatan

Sedangkan plotting antara arus versus waktu selama pengisian kapasitor menghasilkan kurva seperti pada gambar 3 berikut ini.

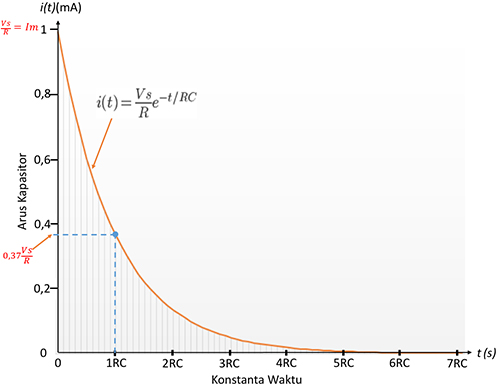Gambar 3. Kurva arus kapasitor versus waktu selama pengisian muatan

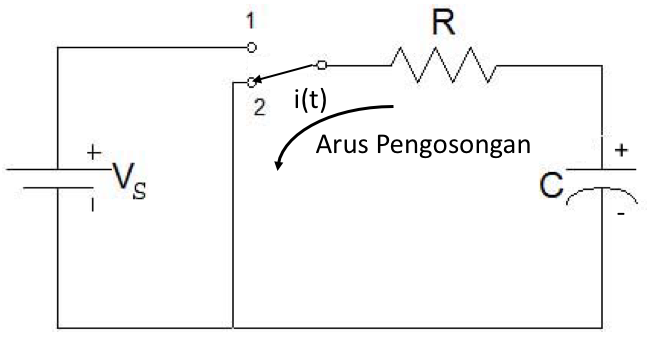
Rangkaian RC Pengosongan Kapasitor

Perhatikan kembali gambar 1 di atas! Pada saat saklar diarahkan ke posisi 1, rangkaian akan membentuk konfigurasi pengisian kapasitor. Andaikata kapasitor telah terisi penuh dengan muatan, saklar kemudian diarahkan ke posisi 2 maka rangkaian akan membentuk konfigurasi pengosongan kapasitor dengan arah arus terbalik menuju ke potensial nol.

Gambar 4. Rangkaian RC Pengosongan Kapasitor

Dalam keadaan seperti ini Vs=0 dan persamaan tegangan menjadi:

$-V_{{R}}-V_{{C}}(t)=0$

$V_{{C}}(t)=-V_{{R}}$ (persamaan 9)

Persamaan dapat diubah dalam bentuk:

$Vc(t)=-i(t)R$

$\frac{Q}{C}=-\frac{dQ}{dt}R $ (persamaan 10)

Seperi halnya pada pegisian kapasitor, persamaan 10 yang menunjukkan arus pengosongan kapasitor dapat diselesaikan dengan metode pemisahan variabel. Dalam hal ini, notasi Q dan dQ ditempatkan pada ruas kiri, sedangkan dt di ruas kanan persamaan, sehingga persamaan 10 dapat diubah menjadi:

$\frac{dQ}{{Q}}=-\frac{1}{RC}dt$

Jika ruas kiri dan ruas kanan diintegralkan, maka persamaan dapat diubah bentuknya menjadi:

$\int_{Q(0)}^{Q(t)} \frac{dQ}{{Q}}=-\frac{1}{RC}\int_{0}^{t}dt $

$ln\left \| Q \right \|| _{Q(0)}^{Q(t)}=-\frac{t}{RC}$

$lnQ(t)-lnQ(0)=-\frac{t}{RC} $

$ln\frac{Q(t)}{Q(0)}=-\frac{t}{RC} $

$e^{ln\frac{Q(t)}{Q(0)}}= e^{-\frac{t}{RC}}$

Berdasarkan sifat bilangan natural, telah diketahui bahwa $e ^{ln(x)}=x$ , sehingga apabila ruas kiri dan ruas kanan dari persamaan di atas menjadi pangkat dari e, maka akan dihasilkan persamaan:

$\frac{Q(t)}{Q(0)}}= e^{-\frac{t}{RC}}$

$Q(t)=Q(0) e^{-\frac{t}{RC}}$ (persamaan 11)

$CV_{{c}}(t)=CV_{{c}}(0)e^{-\frac{t}{RC}}$

$V_{{c}}(t)=V_{{c}}(0)e^{-\frac{t}{RC}}$

Oleh karena pada saat awal pengosongan kapasitor (t=0) nilai tegangan awal pada ujung-ujung kapasitor sama dengan nilai tegangan sumber ( $V_{{c}}(0)=V_{{s}}$ ), maka persamaan dapat ditulis dalam bentuk:

(persamaan 12)

Persamaan 12 menunjukkan tegangan kapasitor selama proses pengosongan muatan (discharging) berlangsung. Persamaan arus pengosongan dapat diturunkan dari persamaan 11. Oleh karena pada proses pengosongan kapasitor arusnya berkurang dari waktu ke waktu maka persamaannya dapat ditulis $i(t)=-\frac{dQ(t)}{dt}$ (tanda negatif menunjukkan arus semakin lama semakin berkurang). Substitusi persamaan ini ke dalam persamaan 11 menghasilkan persamaan:

$i(t)=-\frac{dQ(t)}{dt}=-\frac{dQ(0)}{dt}e^{-\frac{t}{RC}}$

$i(t)=-I(0)e^{-\frac{t}{RC}}$

Pada saat awal (t=0), nilai muatan kapasitor maksimum, sehingga arus awalnya juga maksimum yakni sebesar $\frac{Vs}{R}$ . Persamaan arus pengosongan dapat ditulis;

(persamaan 13)

Persamaan 12 dan persamaan 13 menunjukkan besarnya tegangan dan dan arus kapasitor selama komponen tersebut mengalami pengosongan muatan (discharging). Jika ke dalam kedua persamaan tersebut dimasukkan nilai-nilai variabel t untuk $R=10K\Omega$ dan $C=0,1\mu F$ akan menghasilkan nilai-nilai tegangan dan arus kapasitor seperti ditunjukkan pada tabel 2 berikut ini.

Tabel 2. Nilai tegangan dan arus pada pengosongan kapasitor untuk RC=1ms

Plotting antara Vc versus t akan diperoleh kurva pengosongan kapasitor seperti pada gambar 5 berikut ini.

Gambar 5. Kurva tegangan kapasitor versus waktu selama pengosongan muatan

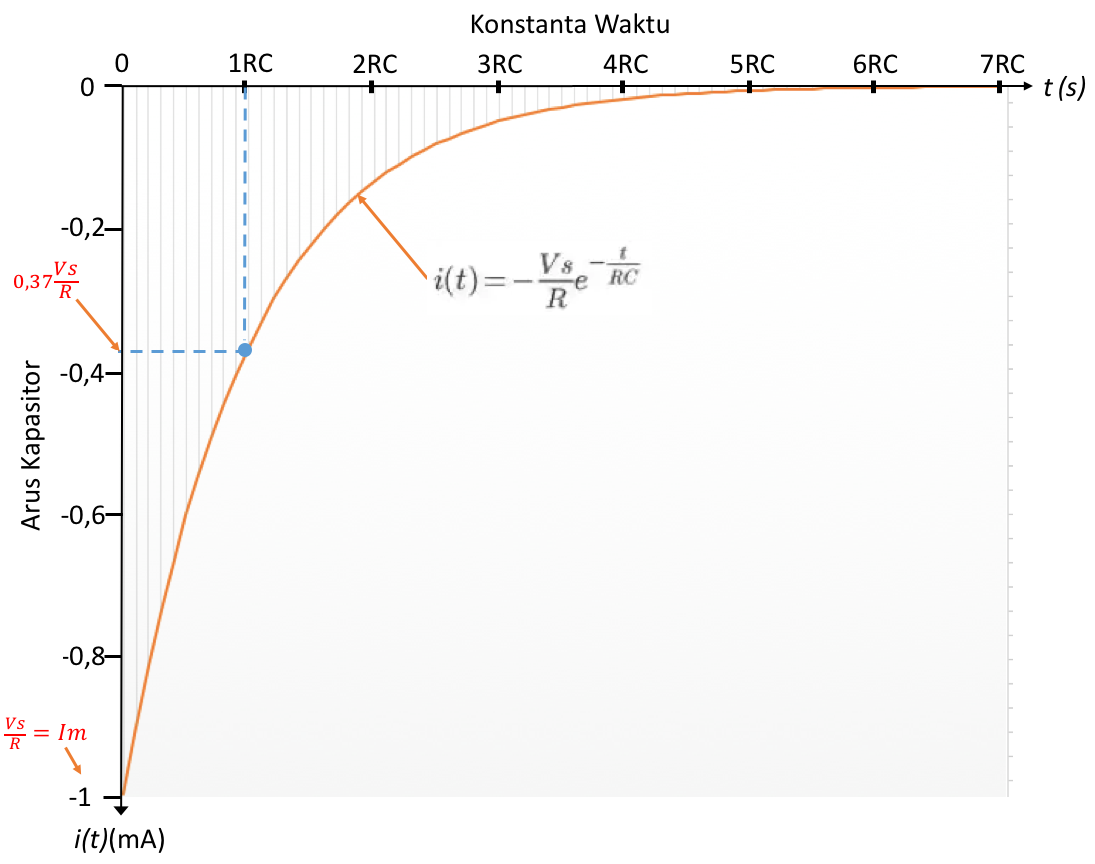
Sedangkan plotting antara arus versus waktu selama pengosongan kapasitor menghasilkan kurva seperti pada gambar 6 berikut ini.

Gambar 6. Kurva arus kapasitor versus waktu selama pengosongan muatan

Simulasi menggunakan PSPICE

Simulasi fenomena pengisian dan pengosongan kapasitor menggunakan PSPICE dapat dilakukan dengan menyusun rangkaian seperti pada Gambar 7.

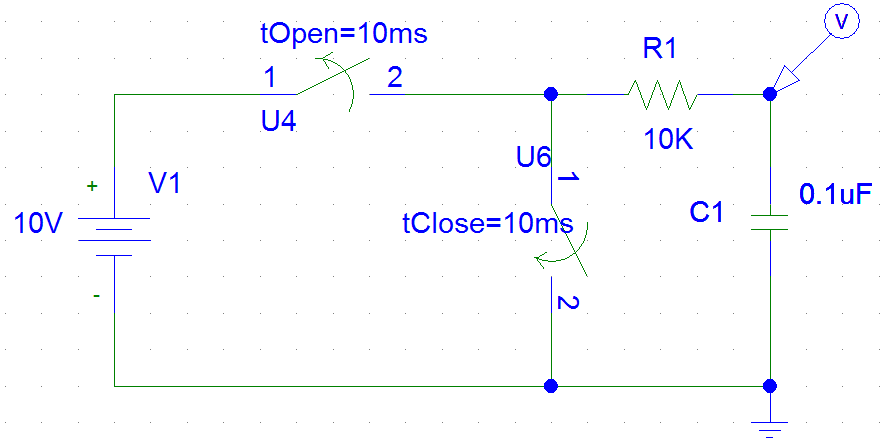
Screen Shot 2018-10-18 at 12.21.25 AM

Gambar 7. Rangkaian Untuk Simulasi Pengisian dan Pengosongan Kapasitor Menggunakan PSPICE Dengan Output Tegangan

Rangkaiannya menggunakan komponen saklar tOpen dan tClose dengan nilai parameter masing-masing 10 ms. Sifat dari kedua saklar tersebut adalah sebagai berikut.

tOpen selalu tertutup, saklar akan terbuka jika diberi nilai parameter tertentu misalnya 10 ms, artinya saklar akan terbuka setelah mencapai waktu10 ms.
tClose memiliki sifat selalu terbuka, jika nilai parameternya diberi 10 ms, kondisinya akan tertutup setelah waktu mencapai 10 ms.

Pengaturan (setting) parameter simulasi agar tampilan grafik proporsional, dapat dilakukan dengan cara:

Hitung terlebih dahulu RC time constant dalam hal ini RC=1ms
Oleh karena kapasitor akan terisi penuh pada t=5RC, maka untuk pengisian kapasitor dapat diberikan waktu simulasi pengisian kapasitor misalnya dua kali 5RC yakni 10ms dan waktu pengosongan juga 10ms sehingga total waktu simulasi sebesar 20ms.
Lakukan pengaturan seperti pada Gambar 8.

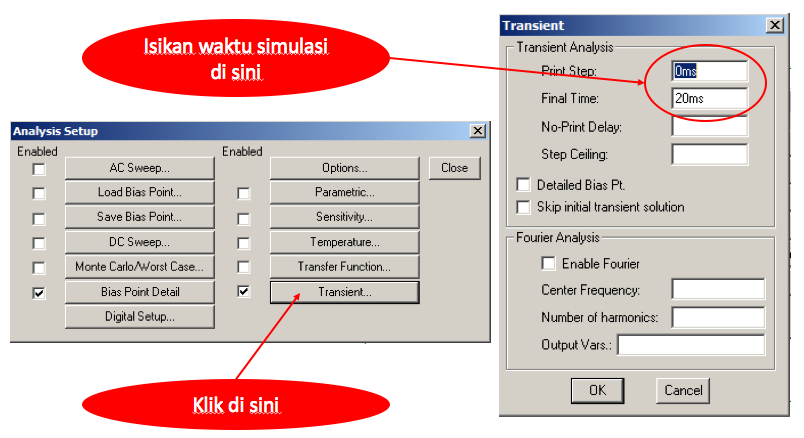
Screen Shot 2018-10-18 at 12.58.25 AM

Gambar 8. Pengaturan Parameter Simulasi Pengisian dan Pengosongan Kapasitor

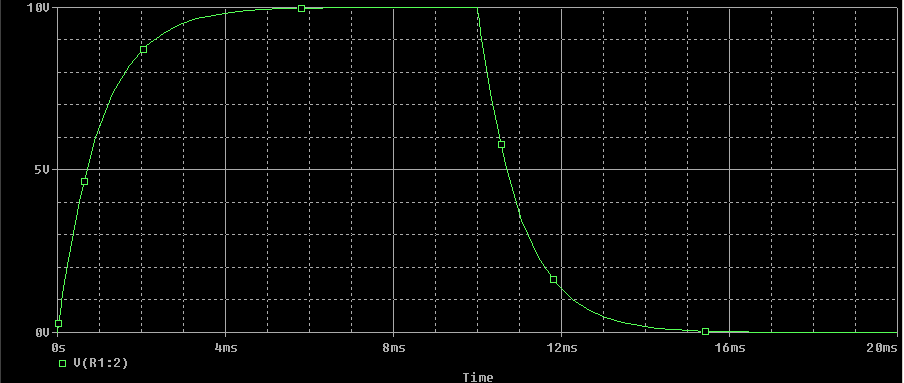
Jika pengaturan tersebut dilakukan dengan benar, maka proses simulasi pengisian dan pengosongan tegangan (rangkaian pada Gambar 7) akan menghasilkan grafik seperti pada Gambar 9.

Gambar 9. Grafik Tegangan Pengisian (t=0 s.d. 10 ms) dan Pengosongan (t=10 s.d. 20 ms) Kapasitor Hasil Simulasi PSPICE

Penampilan grafik arus pada pengisian dan pengosongan kapasitor dapat dilakukan dengan mengganti voltage marker dengan current marker sehingga rangkaian menjadi seperti Gambar 10.

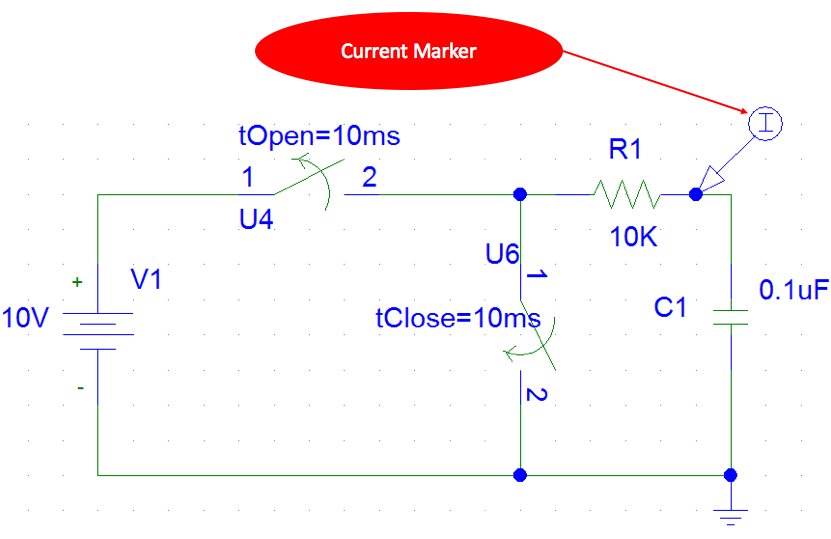
Screen Shot 2018-10-18 at 1.13.27 AM

Gambar 10. Rangkaian Untuk Simulasi Pengisian dan Pengosongan Kapasitor Menggunakan PSPICE Dengan Output Arus

Hasil simulasi dengan menggunakan Gambar 10 ditunjukkan pada gambar 11 berikut ini.

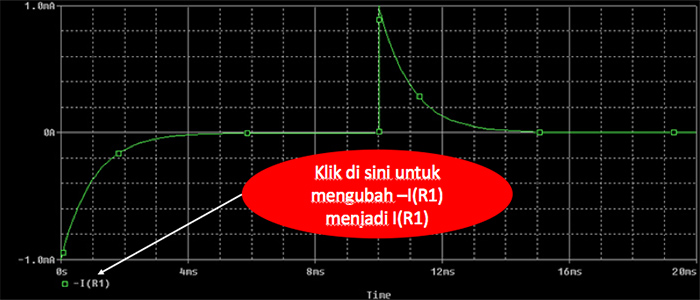
pengosongan-3

Gambar 11. Grafik Arus Pengisian (t=0 s.d. 10 ms) dan Pengosongan (t=10 s.d. 20 ms) Kapasitor Hasil Simulasi PSPICE dengan Variabel terikat -I(R1)

Ubahlah variabel -I(R1) menjadi I(R1) sehingga tampilan grafik menjadi seperti pada gambar 12.

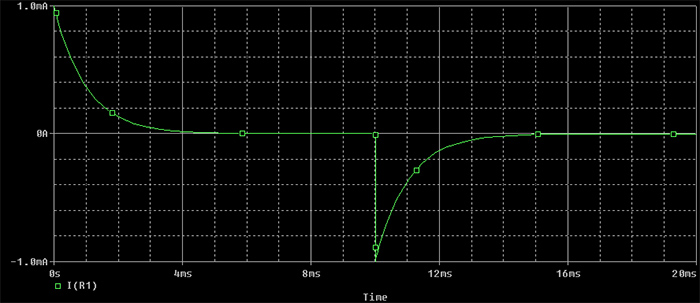
pengosongan4

Gambar 12. Grafik Arus Pengisian (t=0 s.d. 10 ms) dan Pengosongan (t=10 s.d. 20 ms) Kapasitor Hasil Simulasi PSPICE dengan Variabel terikat I(R1)

Sistem Kendali “Stall Detector” dan “Soft Starter” Untuk Aparatus Lab Mesin Listrik

20. September 2018 · Write a comment · Categories: Aktivitas Akademik, Pembelajaran

Sepanjang tahun 2017 saya melakukan riset untuk mengembangkan sistem kendali motor induksi dengan unit stall detector dan soft starter agar dapat digunakan sebagai salah satu unit atau aparatus pada laboratorium Mesin Listrik. Mempertimbangkan aspek efisiensi dan fleksibilitas penggunaan, produk ini diarahkan berbasis SIMULINK, dan untuk lebih mempermudah penyebutan, produk ini selanjutnya disebut dengan Sistem Kendali Motor Induksi Berkinerja Tinggi.

Produk telah melalui proses yang cukup panjang, dari desain sampai dengan implementasi ke dalam model SIMULINK. Sistem juga telah diujikan terhadap 8 (delapan) jenis motor induksi yakni jenis 215 HP, 150 HP, 100 HP, 50 HP, 20 HP, 10 HP, dan 5.4 HP. Hasil pengujian menunjukkan bahwa sistem kendali yang dikembangkan memiliki kinerja yang tinggi sehingga dapat digunakan sebagai apparatus laboratorium Mesin Listrik, ditunjukkan oleh kemampuannya dalam: (1) mereduksi secara signifikan lonjakan arus dan torsi starting yang dibangkitkan motor selama start-up; dan (2) mematikan secara otomatis catu daya ketika motor dalam keadaan stall.

Produk ini juga telah saya presentasikan di hadapan akademisi dan pelaku industri pada seminar nasional teknik elektro di Politeknik Negeri Unjung Pandang, Makasar tanggal 17 September 2018.

20180917_081641 copy

Sesi keynote speech

Produk ini sesungguhnya disiapkan untuk mendukung praktik sistem kendali motor induksi berkinerja tinggi di laboratorium mesin listrik, namun produk juga dapat digunakan oleh mahasiswa jurusan teknik elektro yang ingin belajar secara mandiri.

20180917_121918 copy

Presentasi tentang sistem kendali motor induksi berkinerja tinggi

Selain untuk lingkungan perguruan tinggi, produk ini juga dapat digunakan oleh guru SMK sebagai media pembelajaran materi motor listrik induksi. Naskah publikasi ilmiah secara lengkap dapat diunduh (download) melalui link

http://muchlas.ee.uad.ac.id/v2/profil/penelitian/

sedangkan Panduan dan File Model SIMULINK dari produk dapat diperoleh melalui link:

http://muchlas.ee.uad.ac.id/downloads/motor_control.zip